Chapter 5- Coordinate geometry of a straight line

•  Co-ordinate geometry of a plane

Gradient of a line

Gradient (Slope) of a Straight Line

The gradient ( Also called slope) of a straight line shows how steep a straight line is

The method to calculate the Gradient is:

Divide the change in height by the change in horizontal distance

Gradient  =

Change in Y Change in X

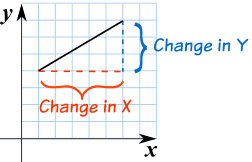Examples:

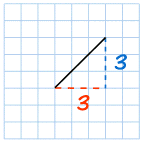The Gradient of this line = 3 3  =  1 So the Gradient is equal to1

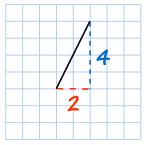	Gradient =	4 2	=  2

The line is steeper, and so the Gradient

is larger.

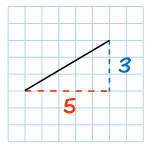		Gradient =	3 5	=  0.6

The line is less steep, and so the 

Gradient is smaller.

Positive or Negative?

Important:

Starting from the left end of the line and going across to the right is positive
(but going across to the left is negative).
Up is positive, and down is negative

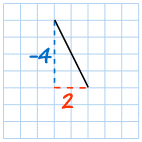	Gradient =	-4 2	= –2

That line goes down as you move

along, so it has a negative Gradient.

Straight Across 

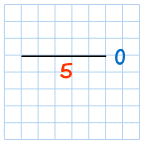	Gradient =	0 5	=  0

A line that goes straight across

 (Horizontal) has a Gradient of zero.

Straight Up and Down

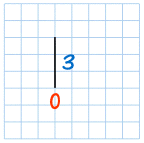	Gradient =	3 0	= undefined

That last one is a bit tricky....you can't divide by zero. So a "straight up and down" ( Vertical) line is gradient is "undefined"

Parallel and perpendicular lines

Parallel and Perpendicular Lines

How to use Algebra to find parallel and 

perpendicular lines.

Parallel Lines

How do we know when two lines are parallel?

Their slopes are the same!

The slope is the value m in the equation of a line: y = mx + b

Example:

Find the equation of the line that is:

• parallel to y = 2x + 1
• and passes though the point (5,4)

The slope of y=2x+1 is: 2

The parallel line needs to have the same slope of 2.

We can solve it using the "point-slope" equation of a line:

y − y₁ = 2(x − x₁)

And then put in the point (5,4):

y − 4 = 2(x − 5)

And that answer is OK, but let's also put it in
 y = mx + b form:

y − 4 = 2x − 10

y = 2x − 6

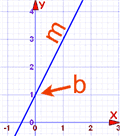Vertical Lines

But this does not work for vertical lines ... I explain why at the end.

Not The Same Line

Be careful! They may be the same line (but with a different equation), and so are not really parallel.

How do we know if they are really the same line? Check their y-intercepts (where they cross the y-axis) as well as their slope:

Example: is y = 3x + 2 parallel to y − 2 = 3x ?

For y = 3x + 2: the slope is 3, and y-intercept is 2

For y − 2 = 3x: the slope is 3, and y-intercept is 2

In fact they are the same line and so are not parallel

Perpendicular Lines

Two lines are Perpendicular if they meet at a right angle (90°).

How do we know if two lines are perpendicular?

When we multiply their slopes, we get −1

Like this:

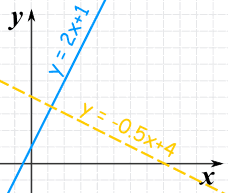
These two lines are perpendicular:

Line	Slope
y = 2x + 1	2
y = −0.5x + 4	−0.5

Because when we multiply the two slopes we get:

2 × (−0.5) = −1

Using It

Let's call the two slopes m₁ and m₂:

m₁m₂ = −1

Which can also be:		m1 = −1/m2
or		m2 = −1/m1

So to go from a slope to its perpendicular:

• calculate 1/slope (the reciprocal)
• and then the negative of that

In other words the negative of the reciprocal.

 

Example:

Find the equation of the line that is

• perpendicular to y = −4x + 10
• and passes though the point (7,2)

The slope of y=−4x+10 is: −4

The negative reciprocal of that slope is:

m = −	1	=	1
	−4		4

So the perpendicular line will have a slope of 1/4:

y − y₁ = (1/4)(x − x₁)

And now put in the point (7,2):

y − 2 = (1/4)(x − 7)

And that answer is OK, but let's also put it in "y=mx+b" form:

y − 2 = x/4 − 7/4

y = x/4 + 1/4

Vertical Lines

The previous methods work nicely except for one particular case: a vertical line:

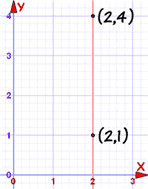
In that case the gradient is undefined (because we cannot divide by 0):

m =

yA − yB xA − xB

=

4 − 1 2 − 2

=

3 0

= undefined

So just rely on the fact that:

• a vertical line is parallel to another vertical line.
• a vertical line is perpendicular to a horizontal line (and vice versa).

Equation of straight line 

 

Equation of a Straight Line

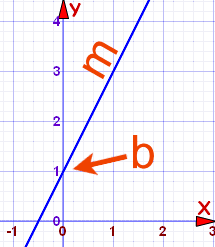
The equation of a straight line is usually written this way:

y = mx + b

(or "y = mx + c" in the UK see below)

What does it stand for?

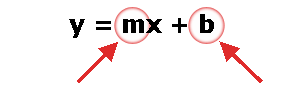Slope (or Gradient)	Y Intercept

y = how far up

x = how far along

m = Slope or Gradient (how steep the line is)

b = the Y Intercept (where the line crosses the Y axis)

How do you find "m" and "b"?

• b is easy: just see where the line crosses the Y axis.
• m (the Slope) needs some calculation:

m =

Change in Y Change in X

Knowing this we can work out the equation of a straight line:

Example 1

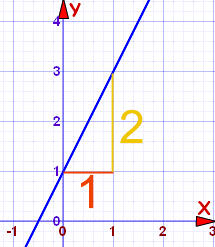
m

=

2 1

=

2

b = 1 (where the line crosses the Y-Axis)

So: y = 2x + 1

With that equation you can now ...

... choose any value for x and find the matching value for y

For example, when x is 1:

y = 2×1 + 1 = 3

Check for yourself that x=1 and y=3 is actually on the line.

Or we could choose another value for x, such as 7:

y = 2×7 + 1 = 15

And so when x=7 you will have y=15 

Example 2

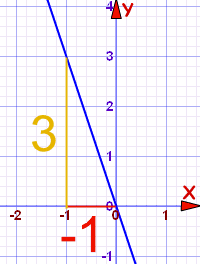
m

=

3 −1

=

−3

b = 0

This gives us y = −3x + 0
We do not need the zero!

So: y = −3x

Example 3: Vertical Line

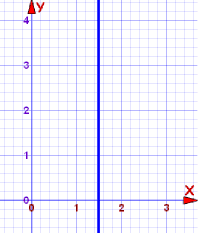
What is the equation for a vertical line?

The slope is undefined ... and where does it cross the Y-Axis?

In fact, this is a special case, and you use a different equation, not "y=...", but instead you use "x=...".

Like this:

x = 1.5

Every point on the line has x coordinate 1.5,

that is why its equation is x = 1.5

Examples

The straight line L1 passes through the points 

(-1, 3) and (11,12).

(a) Find an equation for L1 in the form of 

ax + by + c = 0, where a, b and c are integers.

The line L2 has an equation 3y + 4x - 30 = 0.

(b) Find the coordinates of the point of intersection 

of L1 and L2

Solution

You can also look into

http://mathsathawthorn.pbworks.com/f/Equations+of+straight+lines.pdf